With all the excitement around Apple’s new Swift programming language we were curious whether Swift is suitable for compute-intensive code, or whether it’s still necessary to “drop down” into a lower-level language like C or C++.
To find out we ported three Geekbench 3 workloads from C++ to Swift: Mandelbrot, FFT, and GEMM. These three workloads offer different performance characteristics:
- Mandelbrot is compute bound.
- GEMM is memory bound and sequentially accesses large arrays in small blocks.
- FFT is memory bound and irregularly accesses large arrays.
The source code for the Swift implementations is available on GitHub.
We built both the C++ and Swift workloads with Xcode 6.1. For the Swift workloads we used the -Ofast -Ounchecked optimization flags, enabled SSE4 vector extensions, and enabled loop unrolling. For the C++ workloads we used the -msse2 -O3 -ffast-math -fvectorize optimization flags. We ran each workload eight times and recorded the minimum, maximum, and average compute rates. All tests were performed on an “Early 2011” MacBook Pro with an Intel Core i7-2720QM processor.
| Workload | Version | Minimum | Maximum | Average |
|---|---|---|---|---|
| Mandelbrot | Swift | 2.15 GFlops | 2.43 GFlops | 2.26 GFlops |
| C++ | 2.25 GFlops | 2.38 GFlops | 2.33 GFlops | |
| GEMM | Swift | 1.48 GFlops | 1.59 GFlops | 1.53 GFlops |
| C++ | 8.61 GFlops | 9.92 GFlops | 9.32 GFlops | |
| FFT | Swift | 0.10 GFlops | 0.10 GFlops | 0.10 GFlops |
| C++ | 2.29 GFlops | 2.60 GFlops | 2.42 GFlops |
The Swift implementation of Mandelbrot performs very well, effectively matching the performance of the C++ implementation. I was surprised by this result. I did not expect a language as new as Swift to match the performance of C++ for any of workloads. The results for GEMM and FFT are not as encouraging. The C++ GEMM implementation is over 6x faster than the Swift implementation, while the C++ FFT implementation is over 24x faster. Let’s examine these two workloads more closely.
GEMM
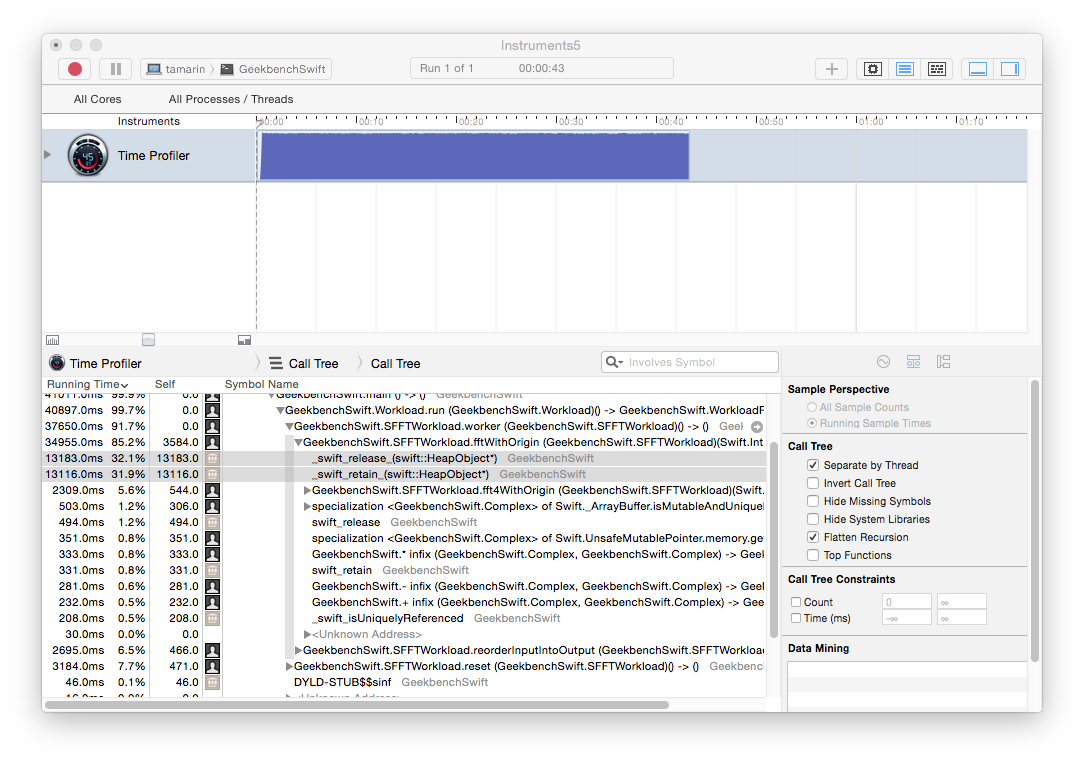
Running GEMM in Instruments (using the Time Profiler template) shows the inner loop dominating the profile samples with 25% attributed to our Matrix.subscript.getter:
Suspecting that the getter was performing poorly I tried caching the raw arrays and accessing them directly without using the subscript getter. This seems to boost performance slightly giving us an average of about 1.55 GFlops. All that remains in the inner loop are the integer operations that compute the indexes, two array reads, one floating point multiply, and one floating point add:
for var k0 = k; k0 < kb; ++k0 {
let a = AM[i0 * N + k0]
let b = BM[j0 * N + k0]
scratch += a * b
}
In our C++ GEMM implementations we get a big performance boost from loop vectorization, so I wondered whether the Swift array implementation might be somehow preventing the LLVM optimizer from vectorizing the loop. Disabling vectorization in the C++ workload (via -fno-vectorize) reduced the average compute rate to just 2.05 GFlops, so loop vectorization is a likely culprit.
FFT
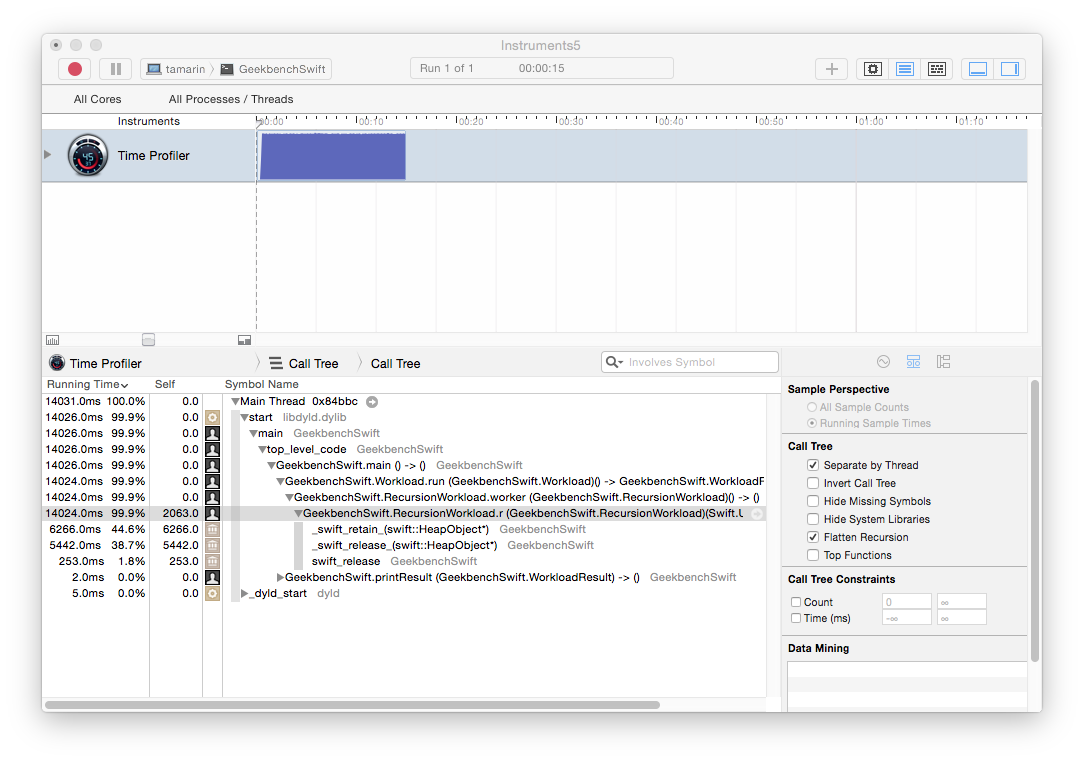
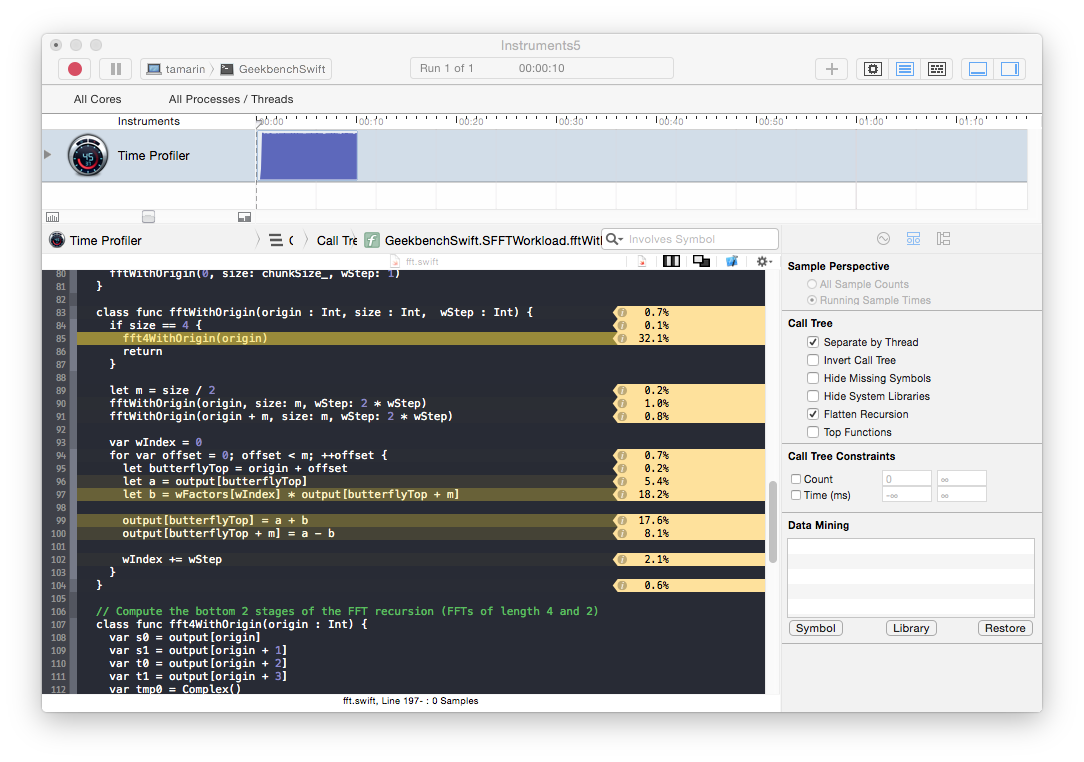
Running FFT in Instruments (again using the Time Profiler template but with the “flatten recursion” option enabled) shows that we spend a lot of time on reference counting operations:
This is surprising because the only reference type in our FFT workload is the FFTWorkload class: arrays are structs and structs are values types in Swift. The FFT workload code reference the FFTWorkload instance using the self member and through calls to instance methods. We begin our investigation here.
To isolate the effects of self references and instance method calls I wrote a recursive function to compute Fibonacci numbers (this is a tremendously inefficient approach to computing Fibonacci numbers, but it is useful for this investigation). I use a self access to count the number of nodes in the recursion by incrementing the nodes member in the recursive function:
func fibonacci(n : UInt) -> UInt {
self.nodes += 1
if n == 0 {
return 0
} else if n == 1 {
return 1
} else {
return fibonacci(n - 1) + fibonacci(n - 2)
}
}
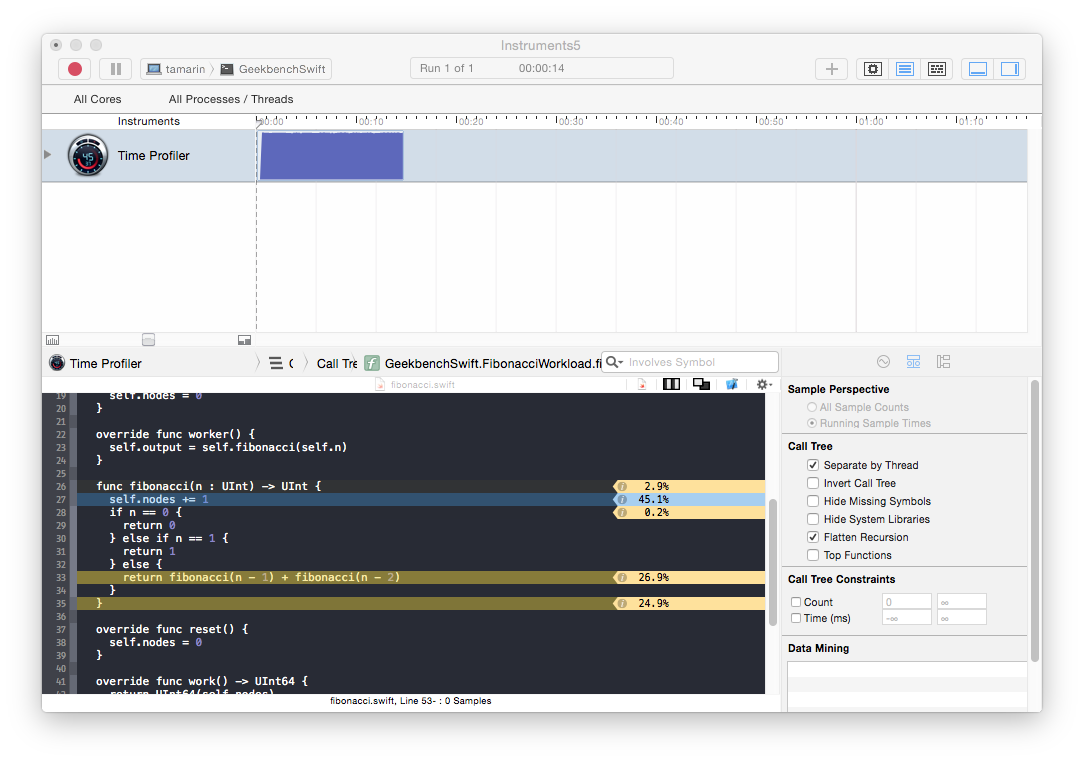
The time profile for this implementation shows a similar effect as observed in the FFT workload.
The source code view suggests that the self accesses are slow in this case:
Updating the recursion to remove references to self nearly doubles performance, but we still see the reference counting operations in the Instruments time profile. This leaves only the method calls.
Next we try making fibonacci a static method instead of an instance method. This is easy since we already removed the self reference: we only need to add the class keyword to the method declaration:
class func fibonacci(n : UInt) -> (f : UInt, nodes : UInt) {
if n == 0 {
return (0, 1);
} else if n == 1 {
return (0, 1);
} else {
let left = fibonacci(n - 1)
let right = fibonacci(n - 2)
return (left.f + right.f, left.nodes + right.nodes + 1)
}
}
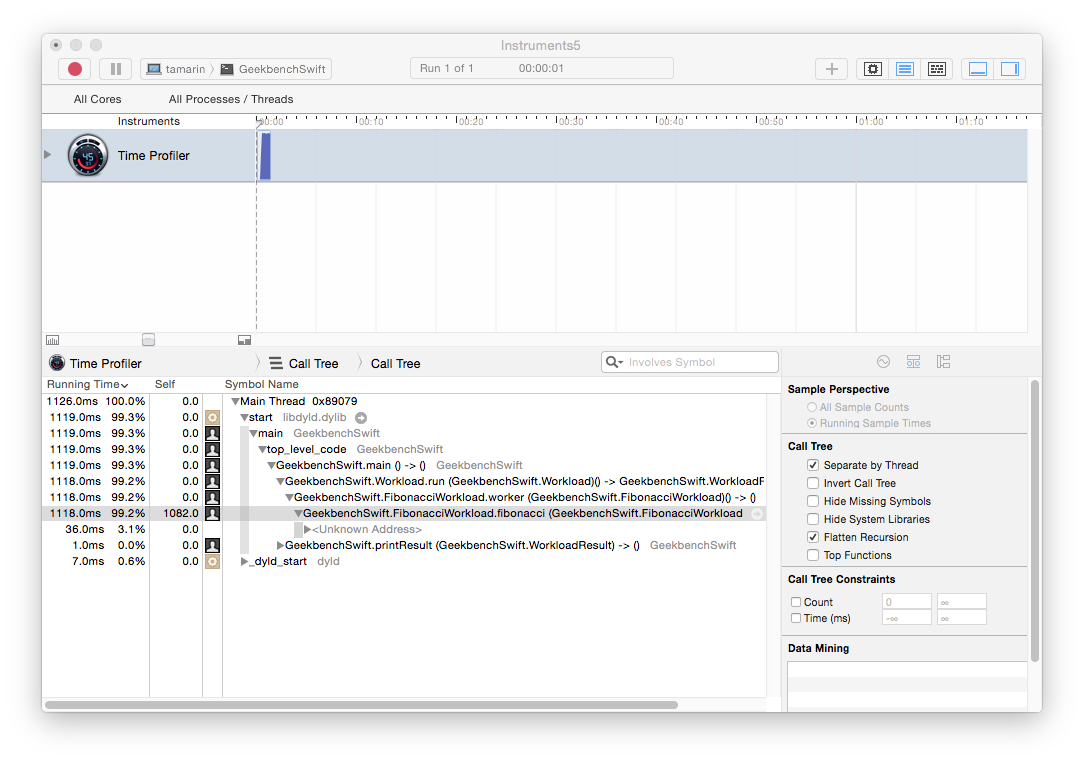
This results in a 12x speedup over the first Fibonacci implementation. The Instruments time profile shows that the reference counting operations are now gone:
I don’t mean to suggest that we should prefer static Swift methods whenever possible; use static method when they make sense in your design. However, if you must implement a recursive algorithm in Swift and you find the performance of your algorithm to be unacceptably poor, then modifying your algorithm to use static methods is worth some investigation.
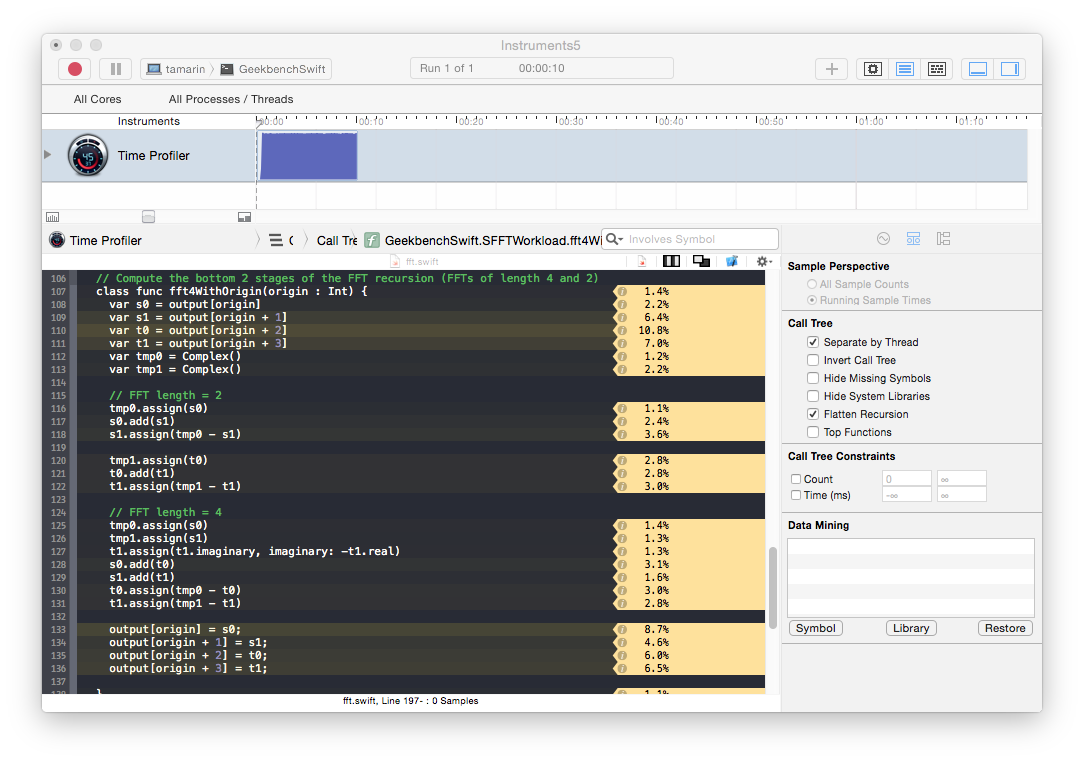
To quickly test this strategy on the FFT workload I made all the instance variables global and changed the recursive methods to class methods. This gives about a 5x boost in performance up to an average of 548.09 MFlops. This is still only about one 20% of the C++ performance, but is a significant improvement. In the time profiler we see that the samples are now more evenly distributed with hotspots on memory access and floating point operations. This is closer to what we might expect for FFT:
Final Thoughts
What can we conclude from these results? The Mandebrot results indicate Swift’s strong potential for compute-intensive code while the GEMM and FFT results show the care that must be exercised. GEMM suggests that the Swift compiler cannot vectorize code that the C++ compiler can vectorize, leaving some easy performance gains behind. FFT suggests that developers should reduce calls to instance methods, or should favor an iterative approach over a recursive approach.
Swift is still a young language with a new compiler so we can expect significant improvements to both the compiler and the optimizer in the future. If you’re considering writing performance-critical code in Swift today it’s certainly worth writing the code in Swift before dropping down to C++. It might just turn out to be fast enough.